Remembering Exact Values
Trig Maths Tips
At some point in trigonometry you'll be told that certain "interesting" angles have "exact" values for their sin, cos and tan. Here's the table of these special trig values in both degrees and radians:
Degrees Radians sin cos tan 30 π/6 1/2 √3/2 1/√3 45 π/4 1/√2 1/√2 1 60 π/3 √3/2 1/2 √3 90 π/2 1 0 None
That's great - until you have to learn them all for a test or exam! If you're like me, one of the reasons you do maths is because you're not very good at memorising stuff. How to go about learning these special values? Here's the way I do it.
How To Remember Trig Values
Rather than learn a weird table of numbers and square roots, I find it best to simply remember two triangles. I'll explain them in degrees, you can easily convert into radians if you prefer.
| Triangle 1 | 
|
|
Imagine a right angled triangle with two 45° angles. It has two angles the same so it's isosceles - assume the two sides are length 1. By
Pythagoras' theorem the hypotenuse must be length √2. Now you can easily get the sin, cos and tan of 45°. Just remember this triangle (or scribble it down) and use standard trig rules (SohCahToa)
|
| Triangle 2 | 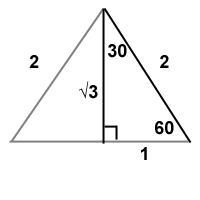
|
|
This one's a little bit more complex but not much, it's still easy to learn. Imagine an equilateral triangle with sides equal to two. Cut it in half. Now you have a 90-60-30 triangle with one side length 1 and hypotenuse 2. By Pythagoras' theorem the other side must be length √3. Now you can use this triangle to quickly get the sin, cos and tan of 30° and 60°.
|
What about 90°? That's the only awkward one, you can't do your normal trig on 90°. But that's the easiest line to learn: "1, 0, none". Certainly a lot easier than trying to remember the whole exact trig functions table!
Check out some more Maths Tips here.